Here is everything you need to know about finding the area of a triangle using trigonometry for GCSE maths (Edexcel, AQA and OCR). You’ll learn how to generate the area of a triangle formula, use the formula to find the area of a triangle and apply this formula to other polygons.
Look out for the Area of a Triangle worksheets and exam questions at the end.
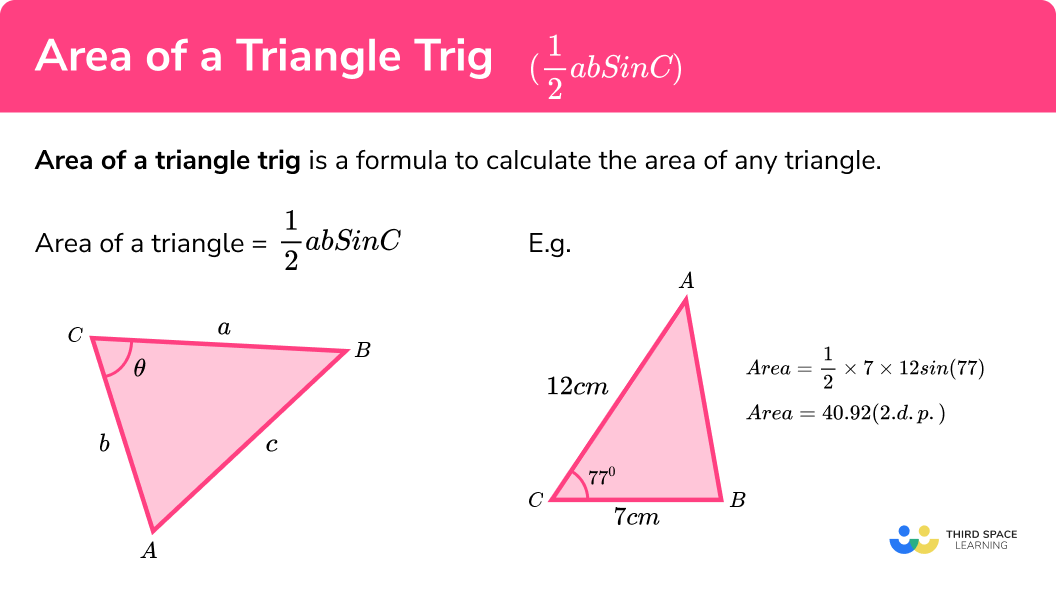
Area of a triangle trig is a formula to calculate the area of any triangle:
\[\text=\fracab\sin C \]Previously, we have calculated the area of a triangle using another formula:
\[\text=\frac \times \text>\]To use this we need to know the vertical height (perpendicular height to the base) of the triangle and the base of the triangle.
We can adapt this formula using the trigonometric ratio \sin(\theta)=\frac to work out the area of a triangle when we do not know its vertical height. The formula we get is:
\[\text=\fracab\sin C\]The triangle should be labelled as follows, with the lower case letter for each side opposite the corresponding upper case letter for the angle.
We need to know:
For example, triangle ABC has been labelled where C is the included angle between the two edges of the triangle a and b .

If we know or can work out the vertical height of a triangle, it can be easier to use the following formula:
\[\text=\frac \times \text>\]However, if the vertical height is not labelled and we know two sides and the angle in between, we would need to use the following:
\[\text=\fracab\sin C\]Once we know which formula to use we need to substitute the correct values into it and then solve the equation to calculate the area. The area is always written with square units.
Remember: other polygons can be split into triangles to find the interior angles,
\[\text=\fracab\sin C\]can be applied to find the area of a rectangle, the area of an equilateral triangle, the area of a pentagon, the area of a parallelogram, etc.
Step by step guide: Angles in polygons.
In order to find the area of a triangle using
\[\text=\fracab\sin C\]


Get your free area of a triangle trig ½abSinC worksheet of 20+ questions and answers. Includes reasoning and applied questions.


Get your free area of a triangle trig ½abSinC worksheet of 20+ questions and answers. Includes reasoning and applied questions.
Calculate the area of the triangle ABC . Write your answer to 2 decimal places.
2 Substitute the given values into the formula
\[A=\frac<1>ab\sin(C)\] \[A=\frac<1>\times12\times7\times\sin(77)\]3 Solve the equation.
\[\beginCalculate the area of the triangle. Write your answer to 2 decimal places.
Label the angle we are going to use angle C and its opposite side c . Label the other two angles A and B and their corresponding side a and b .
Here, we label each side a, b, and c and each vertex A, B and C .
Substitute the given values into the formula.
\[A=\frac<1>ab\sin(C)\] \[A=\frac<1>\times18.2\times10\times\sin(65)\]Solve the equation.
\[\beginCalculate the area of the scalene triangle PQR . Write your answer to 3 significant figures.
Label the angle we are going to use angle C and its opposite side c . Label the other two angles A and B and their corresponding side a and b .
Here, we label each side and each angle.
Substitute the given values into the formula.
\[A=\frac<1>ab\sin(C)\] \[A=\frac<1>\times5.5\times3.6\times\sin(24)\]Solve the equation.
\[\beginTriangle XYZ is an isosceles triangle. Find the area of the triangle to 2 decimal places.
Label the angle we are going to use angle C and its opposite side c . Label the other two angles A and B and their corresponding side a and b .
Here, we label each side and each angle.
Substitute the given values into the formula.
\[A=\frac<1>ab\sin(C)\]As the triangle XYZ is isosceles, b=c .
\[A=\frac<1>\times 9.7\times11.8\times\sin(45)\]Solve the equation.
\[\beginCalculate the area of the triangle ABC. Write your answer to 2 decimal places.

Label the angle we are going to use angle C and its opposite side c . Label the other two angles A and B and their corresponding side a and b .
Here, we label 22 o as C as this angle is between two known sides.
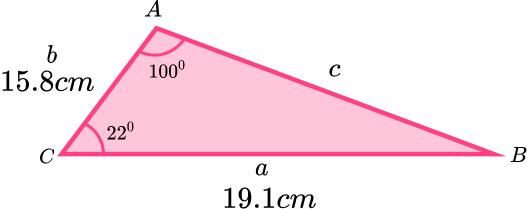
Substitute the given values into the formula.
\[A=\frac<1>ab\sin(C)\]Here, we need to be careful to use the correct angle of C= 22 o .
\[A=\frac<1>\times19.1\times15.8\times\sin(22)\]Solve the equation.
\[\beginCalculate the area of the triangle ABC . Write your answer to 4 significant figures.
Label each angle ( A , B , C ) and each side (a, b , c ) of the triangle.
Here, we have to think carefully because a, b , and C do not correspond to a, b and C in
\[A=\frac<1>ab\sin(C)\]As the known sides b and c have the included angle at A with all three values known, we can adjust the sine rule to make
\[A=\frac<1>bc\sin(A)\]Substitute the given values into the formula.
\[A=\frac<1>bc\sin(A)\] \[A=\frac<1>\times 165\times131\times\sin(9)\]Solve the equation.
\[\beginThe area of this triangle is 30 cm 2 . Find the length labelled x .
Label each angle ( A , B , C ) and each side (a, b , c ) of the triangle.
Substitute the given values into the formula.
\[A=\frac<1>ab\sin(C)\]This time we know the area, one side and the angle.
\[30=\frac<1>\times x\times12\times\sin(38)\]Solve the equation.
\[\beginThe area of this triangle is 42cm 2 . Find the angle labelled x .
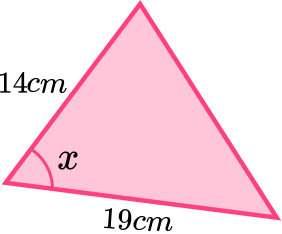
Label each angle ( A , B , C ) and each side (a, b , c ) of the triangle.
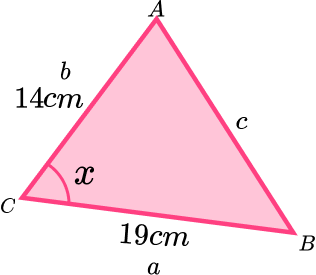
Substitute the given values into the formula.
\[A=\frac<1>ab\sin(C)\]This time we know the area and two sides.
\[42=\frac<1>\times 19\times14 \times\sin(x)\]Solve the equation.
\[\beginWe derive the formula for the area of any triangle by taking the triangle ABC, with vertical height, h:
By applying the usual formula for the area of a triangle (\frac\times\text>) we have A=\frac(a\times) .
We can also state, using trigonometry, that \sin(C)=\frac which we can rearrange to make h the subject h=b\sin(C) .
Substituting h=b\sin(C) into A=\frac(a\times) , we obtain: A=\fracab\sin(C) .
It is important to notice that C is the included angle between the sides of a and b.
Area of a triangle trig is part of our series of lessons to support revision on trigonometry. You may find it helpful to start with the main trigonometry lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
1. Calculate the area of the right angle triangle.




Label the triangle:
\begin \text&=\fracab \sin(C)\\ \text&=\frac \times 21 \times 18 \times \sin(30)\\ \text&=94.5 \mathrm^ \end
2. Calculate the area of the triangle, correct to 2 decimal places.
32.85\mathrm^



Label the triangle:
\begin \text&=\fracab \sin(C)\\ \text&=\frac \times 7.3 \times 9 \times \sin(76)\\ \text&=31.87 \mathrm^ \end
3. Calculate the area of the equilateral triangle XYZ. Write your answer to 2 decimal places.
74.31\mathrm^



Label the triangle:
\begin \text&=\fracab \sin(C)\\ \text&=\frac \times 13.1 \times 13.1 \times \sin(60)\\ \text&=74.31 \mathrm^ \end
4. Calculate the area of the parallelogram, correct to 2 decimal places.
125.41\mathrm^



We need to look at the two triangles individually. The triangles are congruent (exactly the same) since all three of their lengths are equal (SSS). Therefore we can calculate the area of one triangle and then double it.
Label one triangle:
\begin \text&=\fracab \sin(C)\\ \text&=\frac \times 15 \times 22.5 \times \sin(48)\\ \text&=125.406 \mathrm^\\ \text&=2\times125.406=250.81\mathrm^ \end
5. Calculate the area of the isosceles triangle PQR, correct to 3 significant figures.




First, calculate angle PQR: 180-28.3-28.3=123.4 .
Then label the triangle:
\begin \text&=\fracab \sin(C)\\ \text&=\frac \times 6.7 \times 6.7 \times \sin(123.4)\\ \text&=18.7 \mathrm^ \end
6. Calculate the value of \theta




\begin \text &=\fracab \sin(C)\\ 210&=\frac \times 24 \times 35 \times \sin(\theta)\\ 210&=420 \sin(\theta)\\ 0.5&= \sin(\theta)\\ \sin^(0.5)&=\theta\\ 30^&=\theta \end
(2 marks)
Show answer A=\frac<1>\times 8 \times 18 \times \sin(31)(1)
(1)
2. Quadrilateral ABCD is made from two triangles.
a) Work out the length AC .
b) Calculate the total area of the quadrilateral.
(5 marks)
Show answer \begin 11^&=7^+b^\\ b^&=11^-7^ \end(1)
(1)
\text \frac \times 7 \times 8.49 =29.72 \mathrm^
(1)
\begin \text \frac \times 8 \times 8.49 \times \sin(64)\\ \text=30.52 \mathrm^2 \end
(1)
(1)
3. The area of triangle PQR is 55cm^2 . Work out the value of x . Give your answer to 2dp.
(4 marks)
Show answer \frac<1> \times x \times 2x \times \sin(29) = 55(1)
\begin x^ \times \sin(29) &=55\\ 0.485x^&=55 \end
(1)
(1)
(1)
You have now learned how to:
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

© 2024 Third Space Learning. All rights reserved.
Third Space Learning is the trading name of Virtual Class Ltd
We use essential and non-essential cookies to improve the experience on our website. Please read our Cookies Policy for information on how we use cookies and how to manage or change your cookie settings.Accept
Privacy & Cookies PolicyThis website uses cookies to improve your experience while you navigate through the website. Out of these, the cookies that are categorized as necessary are stored on your browser as they are essential for the working of basic functionalities of the website. We also use third-party cookies that help us analyze and understand how you use this website. These cookies will be stored in your browser only with your consent. You also have the option to opt-out of these cookies. But opting out of some of these cookies may affect your browsing experience.
Always EnabledNecessary cookies are absolutely essential for the website to function properly. This category only includes cookies that ensures basic functionalities and security features of the website. These cookies do not store any personal information.
Non-necessaryAny cookies that may not be particularly necessary for the website to function and is used specifically to collect user personal data via analytics, ads, other embedded contents are termed as non-necessary cookies. It is mandatory to procure user consent prior to running these cookies on your website.